How do you apply the ratio test to determine if #sum (1*3*5* * * (2n1))/(1*4*7* * * (3n2))# from #n=1,oo)# is convergent to divergent?In this section we will discuss in greater detail the convergence and divergence of infinite series We will illustrate how partial sums are used to determine if an infinite series converges or diverges We will also give the Divergence Test for series in this sectionCould someone answer please Solve by Arithmetic Progression 1Find the 11th term of 2,4,6 2 Find the sum 135(2n 1)?

Find The Sum To N Term Of The Series 1 3 5 3 5 7 5 7 9
Find the sum of 1+3+5+...+(2n-1)
Find the sum of 1+3+5+...+(2n-1)-Solution for Express the sum 1 3 5 (2n 1) using summation notationUse 1 as the lower limit of summation and i for the index of summationProblem 1 a Calculate 1 35(2n 1 for several natural numbers n ie, the sum of the first n odd numbers (n 2) 3 (n3) 135= (n 4) 1357 b Based on your work in a if n E N, make a conjecture about the value of the sum i' Show the result it true when n = 5 and n = 6 (ie, show P(5) and P(6) are true ii



Sum Of N N Or N Brilliant Math Science Wiki
Weekly Subscription $199 USD per week until cancelled Monthly Subscription $499 USD per month until cancelled Annual Subscription $2999 USD per year until cancelled= 1/ (4n^2 1) as n goes to infinity the bottom goes to a larger and larger number 1/(large number) = small number so it would approach zeroLet's note math(a/mathmath_n)_{n \in \mathbb N^*}/math the sequence Notice that math\displaystyle 1 \times 3 \times 5 \times \ldots \times (2n1)=\frac{1
Problem 1 a Calculate 1 35(2n 1 for several natural numbers n ie, the sum of the first n odd numbers (n 2) 3 (n3) 135= (n 4) 1357 b Based on your work in a if n E N, make a conjecture about the value of the sum i' Show the result it true when n = 5 and n = 6 (ie, show P(5) andAnswer to Write the sum in sigma notation 1) 1357(2n ?(2i1) ?(2i1) 72 72 2 0 2n1 2n ?(i1) i3 2n ?(i1)To find the interval of convergence, note that x−3 < 1 is equivalent to 2 < x < 4, so the endpoints of the interval are x = 2 and x = 4 When x = 2, x − 3 = −1, so the series is given by X∞ n=0 (−1)n (−1)n 2n1 = X∞ n=0 1 2n3, which is a divergent series (do a limit comparison to, eg, P 1 n) When x = 4, x − 3 = 1, so the
Test the convergence of the series \(\Large \sum\limits_{n=1}^{\infty}\frac{135(2n1)}{2462n}x^{n},x\ge 0\)Problem 1 a Calculate 1 35(2n 1 for several natural numbers n ie, the sum of the first n odd numbers (n 2) 3 (n3) 135= (n 4) 1357 b Based on your work in a if n E N, make a conjecture about the value of the sum i' Show the result it true when n = 5 and n = 6 (ie, show P(5) andAnswer is nChange every term in difference of 2 terms by multiplying and dividing by 2After this 2 in numeratorcan be written as=31=53=75=2n12n1 then rationalise every term
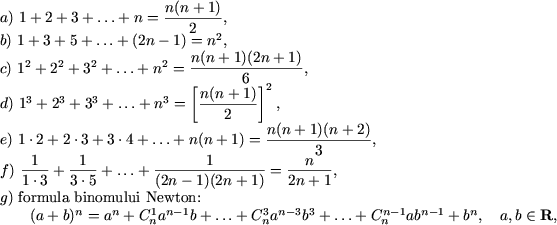


n2 Formula



Notes On Topics Of Algebra Notes
When n = 1, we have (2(1) 1) = 1 2, so the statement holds for n = 1 Step 2 Assume that the equation is true for n, and prove that the equation is true for n 1 Assume 1 3 5 (2n 1) = n 2The sum of part of a series from n 1 to n 2 is 75 The sum of part of the series of natural numbers from n 1 to n 2 is the sum from 1 to n 21 less the sum from 1 to n 2 76 Substituting the formula for the first n natural numbers in 76, we get 77 Which gives us 78 Collecting like terms 79Step 1 Prove true for n=1 LHS= 21=1 RHS=1^2= 1= LHS Therefore, true for n=1 Step 2 Assume true for n=k, where k is an integer and greater than or equal to 1 1357(2k1)=k^2 (1) Step3 When n=k1, RTP 1357(2k1)(2k1)=(k1)^2 LHS 1357(2k1)(2k1) =k^2(2k1) (from 1 by assumption) =(k1)^2 =RHS Therefore, true for n=k1 Step 4 By proof of mathematical



Mathematical Induction Online Presentation



11 4 Series Sigma Notation Ppt Video Online Download
What is the value of the sum 1/1*3 1/3*5 1/5*7 1/7*91/199*1?Given a series 1 2 3 2 5 2 7 2 (2*n – 1) 2, find sum of the series Examples Input n = 4 Output 84 Explanation sum = 1 2 3 2 5 2 7 2 = 1 9 25 49 = 84 Input n = 10 Output 1330 Explanation sum = 1 2 3 2 5 2 7 2 9 2 11 2 13 2 15 2 17 2 19 2 = 1 9 24 49 361 = 1330Find the sum 1 × 3 × 5 3 × 5 × 7 5 × 7 × 9 (2n – 1) (2n 1) (2n 3) Maharashtra State Board HSC Science (Electronics) 11th Textbook Solutions 6926 Important Solutions 17 Question Bank Solutions 4570 Concept Notes & Videos 308 Syllabus



C Exercises Display The Sum Of N Number Of Odd Natural Number W3resource



Sum Of N N Or N Brilliant Math Science Wiki
Our task is to create a program to find the sum of the series 1 (13) (135) (1357) (1357(2n1)) From this series, we can observe that ith term of the series is the sum of first i odd numbersIn this video, we will learn derivation of closed form of the sum of first n odd natural numbersTo derive the closed form of 1 3 5 (2n 1), we wiProblem #3 Find the sum of the following series (1)" 12 2n Σ 42n (2n)!



Find The Sum Of Series Upto N Terms 2n 1 2n 1 3 2n 1 2n
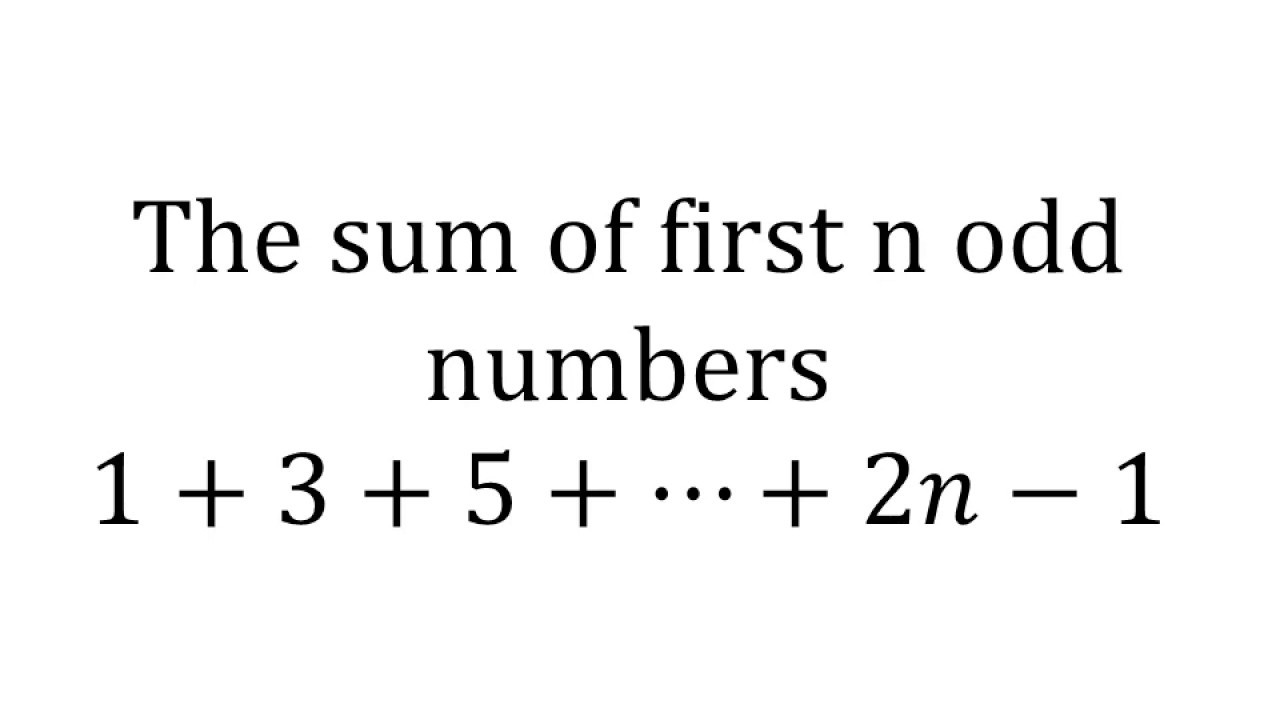


Sum Of First N Odd Natural Numbers 1 3 5 2n 1 Summation Of First N Odd Numbers Youtube
1=0 Problem #3 Enter your answer symbolically, as in these examplesYou have to be very careful with power series They all have a range of values for which they work Consider the power series P = 1 x x^2 x^3 x^4 x^5 x^6 \pm \cdots This is aExpress your answer as a fraction in simplest form


What Is The Sum Of 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 95 97 99 Quora



To Solve The Sum Of The Series 1 3 5 2n 1 Where K 1 To N Nth Term In The Series Graphically By Jimmy Lo Medium
Problem 1 a Calculate 1 35(2n 1 for several natural numbers n ie, the sum of the first n odd numbers (n 2) 3 (n3) 135= (n 4) 1357 b Based on your work in a if n E N, make a conjecture about the value of the sum i' Show the result it true when n = 5 and n = 6 (ie, show P(5) andFor all n∈N, the sum 13 35 57 (2n 1) (2n 1) equals (a) \(\frac{n(2n^23n1)}{6}\ 6}n(n^24)\) (d) \(\frac{1}{3}n^2(4n^25)\)My attempt is to deduce a formula for simplifying $\frac{n}{(1)(3)(5)(7)(2n1)}$ by lookin Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers


What Is The Sum Of The Series 1 1 3 5 1 3 5 7 1 5 7 9 Up To N Terms Quora



Sum Of The First N Odd Numbers Is N 2 Mathematics Stack Exchange
Let's note math(a/mathmath_n)_{n \in \mathbb N^*}/math the sequence Notice that math\displaystyle 1 \times 3 \times 5 \times \ldots \times (2n1)=\frac{1Show that 135(2n1) = n2, where n is a positive integer Proof by induction Inductive step (Show k (P(k) P(k1)) is true) Assume P(k) is true Use mathematical induction to prove the formula for the sum of a finite number of terms of a geometric progression ark = aarar2arn= (arn1 a) / (r1) when r 11calculate 135(2n1) for several natural numbers n 2based on your work in previous question, if n ∈ N, make a conjecture about the value of the sum 135(2n1)= n (on top of sigma and below sigma) j=1, and in the middle of sigma (2j1) 3 use mathematical induction to prove your conjecture in problem #2


Mple 2 17 Find The Sum Of The First 2n Terms Of The Followin Scholr



File The Sum Of The First N Odd Integers Is N 1 3 5 2n 1 N Gif Wikipedia
Click here👆to get an answer to your question ️ Find the sum of n→∞ ( 1/13 1/35 1/(2n1)(2n1))We can square n each time and sum the result 4 Σ n=1 n 2 = 1 2 2 2 3 2 4 2 = 30 We can add up the first four terms in the sequence 2n1 4We can square n each time and sum the result 4 Σ n=1 n 2 = 1 2 2 2 3 2 4 2 = 30 We can add up the first four terms in the sequence 2n1 4



Solved Write The Sum In Sigma Notation 1 3 5 7 Chegg Com



Solved Find The Sum Of The Series 1 1 3 1 3 5 1 5 7 Chegg Com
(2n1) = 3 5 7 9 = 24 And we can use other letters, here we use i and sum up i × (i1), going from 1 to 3 3= (2n) 3 – 3 (2n) 2 1 31 22n1 3 Since, (ab) 3 = a 3 – 3a 2 b 3ab 2 – b = 8n 3 – 12n 2 6n – 1 Now, let S n be the sum of n terms of the given seriesMy attempt is to deduce a formula for simplifying $\frac{n}{(1)(3)(5)(7)(2n1)}$ by lookin Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers



Find The General Term And The Sum Of N Terms Of The Series 3 1 1139 167



Chapter 10 Mathematical Induction People Vcu Edu
Click here👆to get an answer to your question ️ Find the sum of n→∞ ( 1/13 1/35 1/(2n1)(2n1))`sum_{n=1}^5(2n1)` `=` `=25` Notice that the expression (2n − 1) generates odd numbers as n takes values 1, 2, 3, 4, 5 If we want to generate evenSum of first three odd numbers = 1 3 5 = 9 (9 = 3 x 3) Sum of first four odd numbers = 1 3 5 7 = 16 (16 = 4 x 4) Step 2 The number of digits added collectively is always equal to the square root of the total number Sum of first odd number = 1 The square root of 1, √1 = 1, so, only one digit was added Sum of consecutive two odd


Sum Of Natural Numbers



Ex 4 1 17 Prove 1 3 5 1 5 7 1 7 9 1 2n 1 2n 3
Prove that 135(2n1)= (n1) 2 for all n greater than or equal to 1 Hi Emma, Suppose that we use S to designate this sum, that is S = 1 3 5 (2n1) There is a nice way to evaluate S that starts with evaluating 2S by writing the sum forwards and and then backwardsAnswer to 1 Write the first 5 terms {Sn} = {2n / 3n 1} 2 Find the sum of the sequence 10 Σk2 4 k= 1 3 Determine whetherProve that 135(2n1)= (n1) 2 for all n greater than or equal to 1 Hi Emma, Suppose that we use S to designate this sum, that is S = 1 3 5 (2n1) There is a nice way to evaluate S that starts with evaluating 2S by writing the sum forwards and and then backwards



Proof By Induction Help Mainly 2a 2b 2c And 14a With 2a I Got Stuck When K2 2k 1 Should Equal The Sum With Number 14 I Am Totally Lost



Find The Sum Of The Series 2 3 5 9 8 15 11 21 To 2n 1 Terms Youtube
3 MATHEMATICAL INDUCTION Which shows 5(n 1) 5 (n 1)2By the principle of mathematical induction it follows that 5n 5 n2 for all integers n 6 Discussion In Example 341, the predicate, P(n), is 5n5 n2, and the universe of discourse is the set of integers n 6(2n1) = 3 5 7 9 = 24 And we can use other letters, here we use i and sum up i × (i1), going from 1 to 3 3(2n1) = 3 5 7 9 = 24 And we can use other letters, here we use i and sum up i × (i1), going from 1 to 3 3



Find Sum Of Series 1 3 5 7 9 11 Upto N Terms When Brainly In
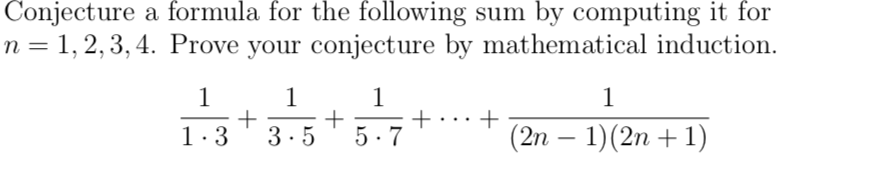


Solved Discrete Mathematics Conjecture A Formula For Th
Let's note math(a/mathmath_n)_{n \in \mathbb N^*}/math the sequence Notice that math\displaystyle 1 \times 3 \times 5 \times \ldots \times (2n1)=\frac{1The next term of the sequence, ie the (n1)th term 1, 3, 5, , (2n1) which is summed is (2n1), now with n=1 the relationship, 1 3 5 (2n1) = n^2 (1) holds obviously since both sides are 1 Now say (1) holds for n = k for some positive integer k, then, 1 3 5 (2k1) = k^2 add the next term (2k1) to both sides, then;If the given sequence is 1, 3, 5, 7, Then the series will be 1 3 5 7 And we will write it as S n = 1 3 5 7 Types of Series The different types of series are Arithmetic Series



Answered And N 2n 1 N 1 3 5 13 The Bartleby



Solved 3 Prove That 1 3 5 2n 1 N2 For Al Chegg Com
My attempt is to deduce a formula for simplifying $\frac{n}{(1)(3)(5)(7)(2n1)}$ by lookin Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careersShow that 135(2n1) = n2, where n is a positive integer Proof by induction Inductive step (Show k (P(k) P(k1)) is true) Assume P(k) is true Use mathematical induction to prove the formula for the sum of a finite number of terms of a geometric progression ark = aarar2arn= (arn1 a) / (r1) when r 1The next term of the sequence, ie the (n1)th term 1, 3, 5, , (2n1) which is summed is (2n1), now with n=1 the relationship, 1 3 5 (2n1) = n^2 (1) holds obviously since both sides are 1 Now say (1) holds for n = k for some positive integer k, then, 1 3 5 (2k1) = k^2 add the next term (2k1) to both sides, then;



Find The Sum 1 3 3 5 5 7 Upto N Term Brainly In



Ex 4 1 7 Prove 1 3 3 5 5 7 2n 1 2n 1 Class 11



Ex 9 4 10 Find Sum Of Series Nth Terms Is 2n 1 2 Ex 9 4


Natural Numbers Series 14 3 Sideway Output To


What Is The Sum Of 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 95 97 99 Quora



Convergent Divergent Geometric Series With Manipulation Video Khan Academy


Prove The Following By Using The Principle Of Mathematical Induction For All N N 1 3 3 5 5 7 2n 1 2n 1 N 4n 2 6n 1 3 Sarthaks Econnect Largest Online Education Community


Natural Numbers Series 14 3 Sideway Output To
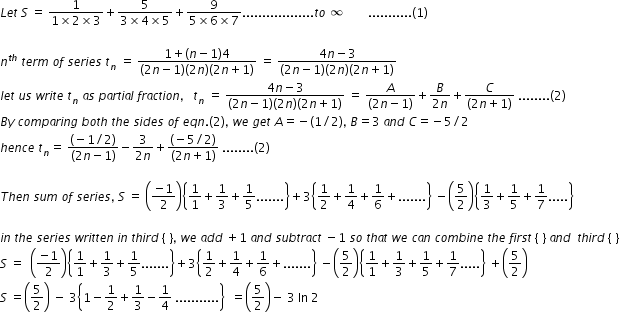


Q1 Sum Of The Series 1 123 5 345 9 567 Till Infinity Q2 Find Value Of Log 1 1 N N Mathematics Topperlearning Com Qyqyjc



Answered A Fill In The Blank 1 3 5 Bartleby


What The Sum Of 1 1 2 1 3 2 1 5 2 1 2n 1 2 Quora



Sum To N Terms 2n 1 2 2n 3 3 2n 5 Youtube



Find The Sum To N Term Of The Series 1 3 5 3 5 7 5 7 9



Illustration 19 Find The Sum Of N Terms Of The Series 1 3 5 3 5 7 5 7 9 Solution The Nth Term Is 2n 1 2n 1 2n 3 T 2n



Solved Usins Iiduclioln Verily Thal Cacil Eqtal Is Elor Chegg Com



Question Can You Prove 1 3 5 2n 1 Chegg Com


What Is The Proof Of Math 1 3 3 5 5 7 2n 1 2n 1 N 4n 2 6n 1 3 Math By Using The Principle Of Mathematical Induction Quora



Find The Sum Of Series Upto N Terms 2n 1 2n 1 3 2n 1 2n 1 2 5 2n 1 2n 1 3 Youtube



If The Nth Term Of An Ap Is 2n 1 Then The Sum Of Its First Three Terms Is Youtube



Number Sequences Overhang This Lecture We Will Study Some Simple Number Sequences And Their Properties The Topics Include Representation Of A Sequence Ppt Download



Find The Sum Of 1 1 3 5 1 3 5 7 1 5 7 9 Up To N Terms



5 1 Sequences And Summation Notation T



Find The Sum Of The Following Series Up To N Terms 1 3 1 1 3 2 3 1 3 1 3 2 3 3 3 1 3 5 Mathematics Shaalaa Com



The A M Of 1 3 5 2n 1 Is



Grade 10 Math What The Frick Why Is The Sum Of This Arithmetic Series N 2 2n Homeworkhelp



Tips And Tricks To Solve Sequences And Series Questions Advanced



Ex 1 Infinite Series The Ratio Test Convergent Cute766



Rd Sharma Solutions For Class 11 Chapter 19 Arithmetic Progressions Download Free Pdf



Sum Of Squares Of Odd Numbers 1 2 3 2 5 2 2n 1 2 Derivation Formula Prmo Rmo Iit Youtube



Which Is The Largest Number In The Following Sequence 1 1 Sqrt



T K Rengarajan 4 A Visual Proof That The Sum Of The First N Odd Numbers Is N 2 1 3 5 2n 1 N 2 Math Is Mysterious Mathisbeautiful T Co Hui31vvztj



Sum Of N Squares Part 2 Video Khan Academy



Ex 4 1 17 Prove 1 3 5 1 5 7 1 7 9 1 2n 1 2n 3



What Is The Sum Of This Series 1 3 5 7 9 99 Brainly In



Maths Zone Sum Of First N Odd Numbers Is N 2 Facebook



Solved Problem 1 A Calculate 1 3 5 2n 1 For Several Chegg Com



Problem 8 Score 25 A 25 Points Prove By Induction The Following Partial Sum Equation 1 1 Homeworklib



Sequence Function



1 1 2 1 4 1 N Sum Formula
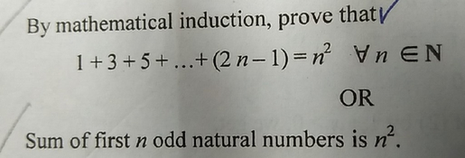


By Mathematical Induction Prove Thaty 1 3 5 2n 1 N2 Yn Scholr



Og 3 S Lo N3 2 Cos Kvk2 1 K 1 0o 7 Find The Exact Chegg Com



Prove That 2n 1 N 2 N 1 3 5 2n 1 2n 1 Youtube


Find The Sum Of First N Odd Natural Numbers Sarthaks Econnect Largest Online Education Community
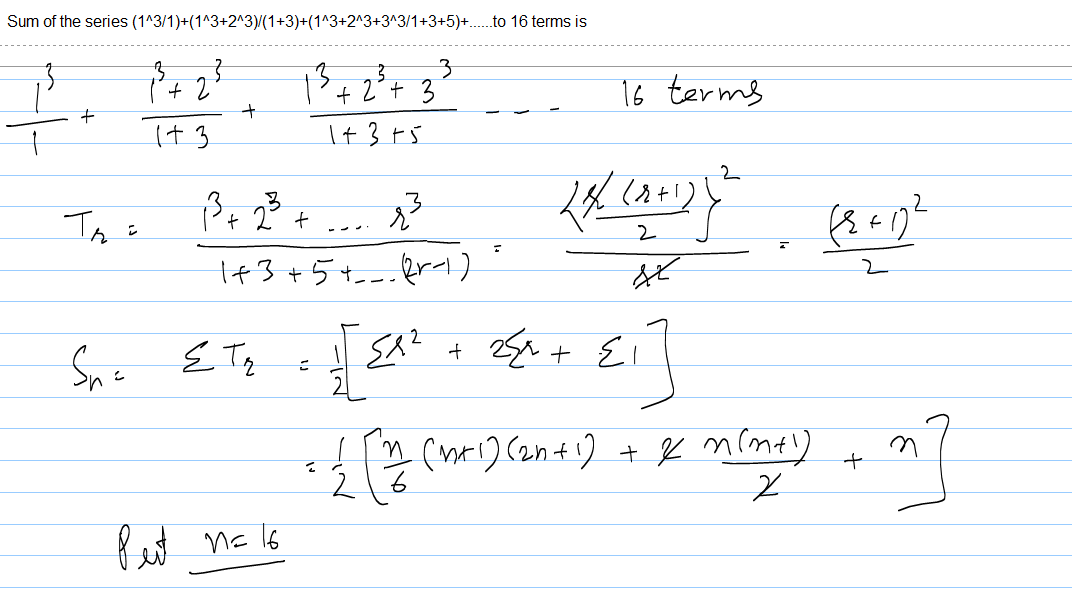


Sum Of The Series 1 3 1 1 3 2 3 1 3 1 3 2 3 3 3 1 3 5 To Askiitians



Find The Sum Of Series Upto N Terms 2n 1 2n 1 3 2n 1 2n
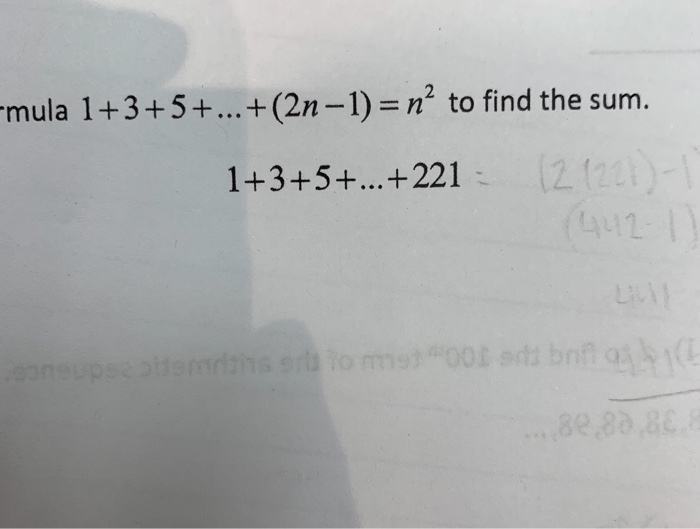


Solved Mula 1 3 5 2n 1 N To Find The Sum 1 3 5 Chegg Com



Ppt Aops Powerpoint Presentation Free Download Id



1 2 3 2 5 2 2n 1 2 Br N 2n 1 2n 1 3



Solved Evaluate The Sum Of The Following Series Summatio Chegg Com
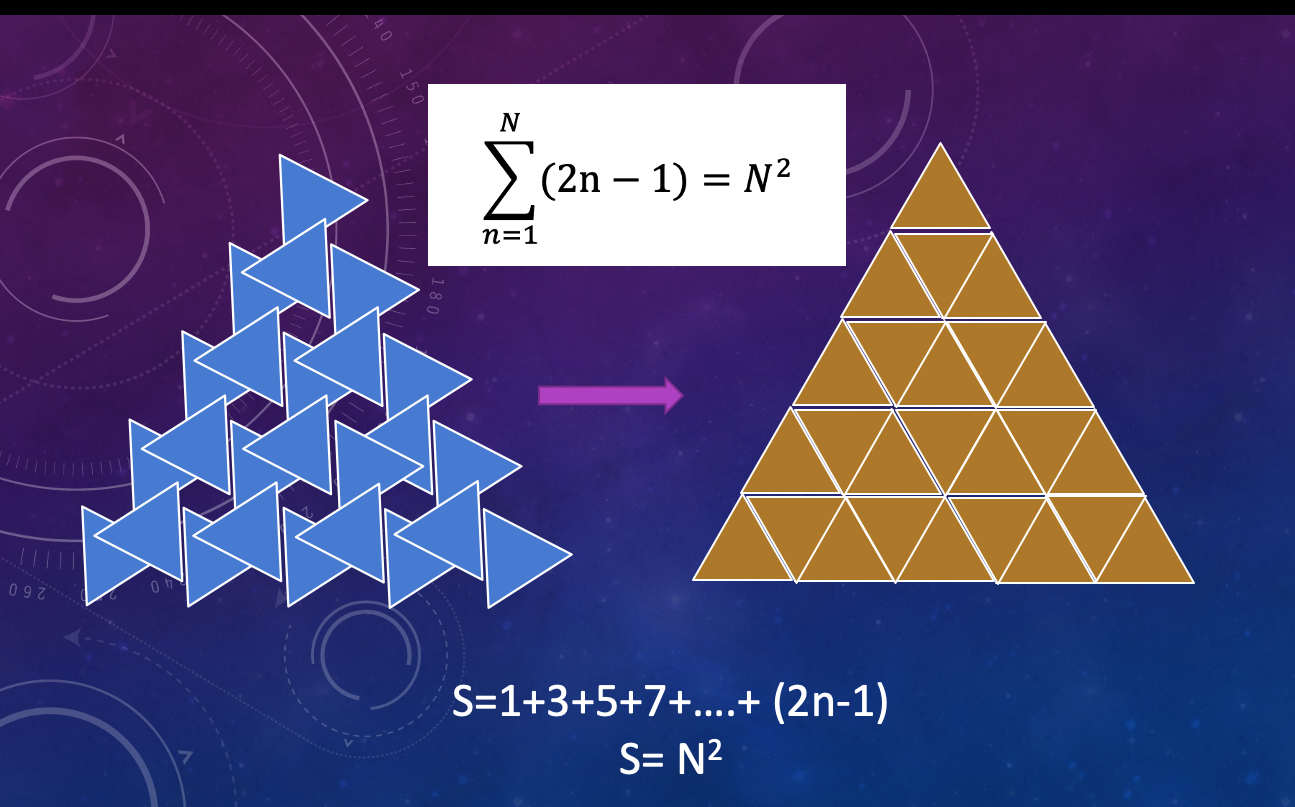


To Solve The Sum Of The Series 1 3 5 2n 1 Where K 1 To N Nth Term In The Series Graphically By Jimmy Lo Medium



Problem 8 Score 25 A 25 Points Prove By Induction The Following Partial Sum Equation 1 1 Homeworklib



7 Proof By Induction 1 3 5 7 2n 1 N 2 Discrete Prove All N In N Induction Mathgotserved Youtube


How To Evaluate The Sum Of N 2 2 N From N 1 To Infinity Quora



Preliminary To Math Induction An Infinite Sequence Of Propositions



Terms 25 Find The Sum Of The Following Series Up To 11 221 23



Ex 4 1 7 Prove 1 3 3 5 5 7 2n 1 2n 1 Class 11



1 13 1 25 1 N 2n 1 Mathematics Topperlearning Com 1zm9zzrr



Find The Sum To N Terms 1 2 3 2 5 2 Youtube



Sum Of N Terms Of The Series 2n 1 2 2n 3 3 2n 5 Is


Natural Numbers Series 14 3 Sideway Output To



Divergence Of The Sum Of The Reciprocals Of The Primes Wikipedia
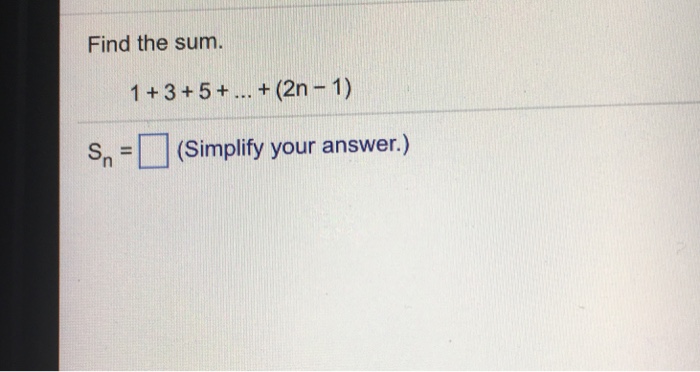


Solved Find The Sum 1 3 5 2n 1 Sn Simplify Yo Chegg Com



Practice For Exam 2 Math 3410


How To Prove That Math 1 3 3 3 5 3 2n 1 3 2n 4 N 2 Math Using Mathematical Induction Quora


Tamas Gorbe Applying Vieta S Formula 3 And Simplifying The Binomial Coefficients Yield Cot P 2n 1 Cot 2p 2n 1 Cot Np 2n 1 N 2n 1 3 Using Csc A Cot A 1 Turns The Above Sum Into



Solved Show That The Sum Sn Of The First N Terms Of The S Chegg Com



0 件のコメント:
コメントを投稿